折現率 是什麼?為什麼我們要理解折現率(貼現率)的觀念?了解折現率對於財務分析和投資決策非常重要。折現率能夠幫助我們將未來現金流量的價值轉換為現在的價值,並考慮到時間價值的影響。理解折現率,能讓我們在理財這個領域中,看待事情的角度,產生了變化,進而做出更符合人生價值觀的決策。因此在以下的文章,我們將介紹折現率的觀念,以及分享日常生活中常見的使用場景,進而更加活用。
Table of Contents
折現率是什麼?
折現率對投資理財來說非常重要。為什麼要理解折現率?因為在一般的情況,我們會在同一個時間點比較兩個金錢價值,但是在論及理財或投資的觀點時,幾乎都會加上時間這項變數,因為我們會去評估未來的資產成長、或是不同決策的價值。
好比現在投資10萬元,10年之後變成20萬元;或是你想跟銀行借一筆為期20年100萬的房貸,這些例子都內含折現率的存在。
然而,就是因為在不同時間,貨幣所代表的價值會有所不同,我們並沒有辦法直接將金額大小做直接的比較。像是30年前的100萬元,跟現在的100萬元,你絕對不會說他們代表的價值是相同的,畢竟前者可能買下一棟房子,而現在的100萬元,可能只能買到一坪。
所以當我們要將未來的現金價值轉換為目前的現金價值,折現率便是陳述這兩者之間的關係,或者是說,折現率用來表示不同時間的貨幣價值關係。
我們常見的PV(Present Value),稱為現值,而終值FV(Future Value),則是未來的貨幣價值,折現率就是計算這兩者之間的一項比率。
貼現率怎麼算?
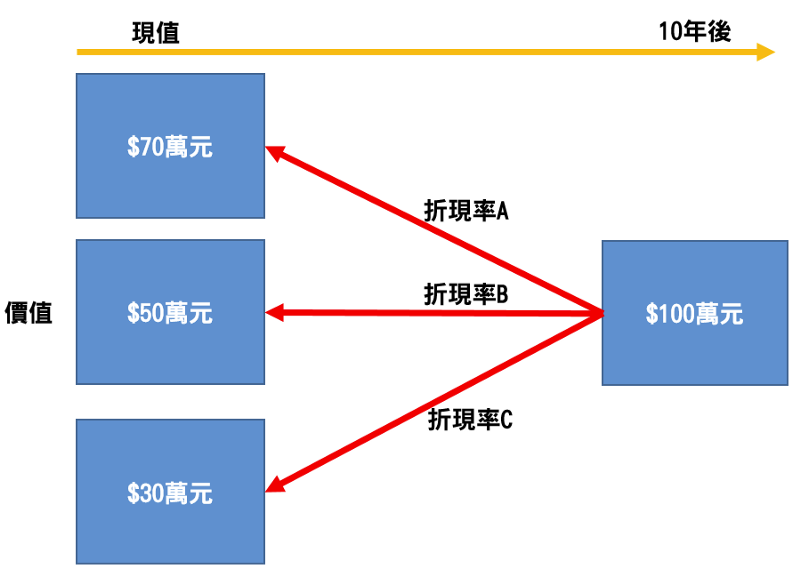
想一想關於這個問題:「現在的100萬元還是10年後的100萬元比較值錢?」
你會很直覺地說,現在的100萬元比較值錢。如果再進一步問你為什麼?你很可能會回答,因為通貨膨脹的關係,物價會越來越貴,同樣的金額,在未來的時代,能買的分量會越來越少。所以,現在的100萬元比較值錢。
沒有錯。
那我們再假設一個情境:有一天,你對兒子說:兒子阿,10年後爸爸準備了100萬給你,開不開心?沒想到兒子竟然回答說:不開心,現在就給我錢。
身為孩子爸的你,已經懂得10年後的一百萬跟現在的一百萬,是不同量級的價值,但為了滿足兒子的願望,你願意改成當下給予多少錢呢?
我們都知道不同時代的貨幣價值不同,而從未來換算到現在的貨幣價值的比率,就稱為折現率。
從上述的例子來看,假如你後來決定給兒子50萬元,那關於折現率的算法便是
- 現值 (現在的錢)* (1 + 折現率) ^ 年數 = 終值(未來的錢)
- 50萬 * (1+折現率)^10(年) = 100萬
- (1+折現率)¹⁰ = 2
- 折現率 ~= 7.177%
換句話說,當你認為貨幣的價值,約莫每年貶值7.177%左右,則現在的50萬元將會等同10年後的100萬元,而7.177%就是所謂的折現率。
因此,折現率是一種比值,用來說明現在的貨幣,與未來貨幣的價值交換關係。當折現率越大,表示未來貨幣價值貶值的速度越快,比如10%的折現率,現在的100元會等於30年後的17449元;而當折現率越小,則貶值的速度越慢,1%的折現率,現在的100元會等於30年的1347元。
同樣的100元,在不同的折現率之情境,代表的價值會更不同。
折現率的應用
通貨膨脹
你現在存的錢,在未來將會賠錢,我認為通貨膨脹就是最好的運用例子。
許多人的理財方式,是將工作辛苦賺來的錢存入銀行中,存錢是美德,在不懂投資之前,存錢確實是最好的理財方式。但是過於保守的投資,卻往往會讓辛苦累積的錢失去原本應有的價值。
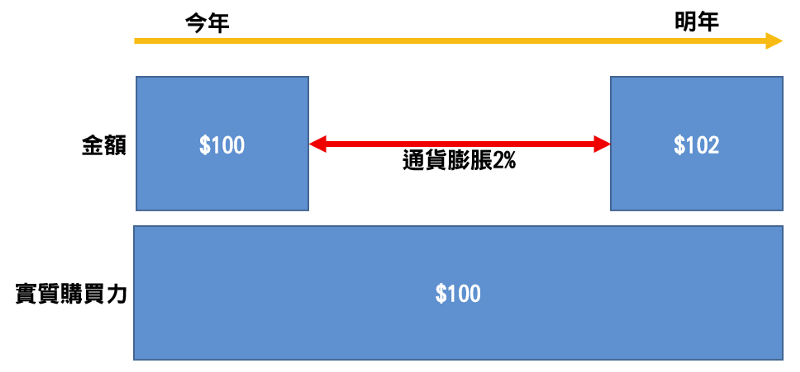
台灣的通貨膨脹率,長期下來約為2%左右,換句話說,每年的物價平均會上漲2%。我們都曉得,一旦東西變貴,而錢包的錢沒有隨著變多,這便是所謂的實質購買力下降,換句話說,原本100元的購買力,到了明年,卻無法辦法購買同等價值100元的物品。
然而,為了擁有相同購買力的我們,該準備多少錢才夠用買到現在100元的東西呢?
可以套用先前的公式計算
- 現在的錢 * (1 + 折現率) ^ 年數 = 未來的錢
- 100*1.02^1=102
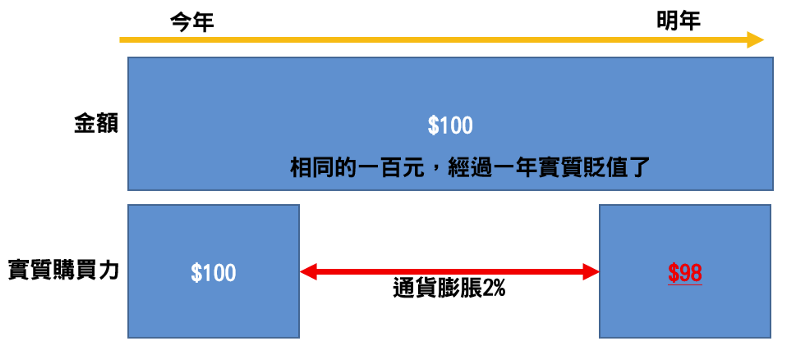
透過折現率的計算,明年的102元才會等同於今年的100元,這個意思是,明明都是新台幣,但是錢卻變薄了,明年的100元必須多兩元才會跟今年的100元相同價值。
換言之,明年要買到今年價值100元的產品,我們得準備102元才行,而過於保守的投資,所產生的問題就是在這。
當今年的我們,僅僅只是存錢,是不可能讓100元平白變成102元的,這便是通貨膨脹,背後所隱含的折現率情境。
因此,一旦我們無法讓貨幣增加的速度,跑贏通貨膨脹的速度,那我們現在存的錢,注定在未來就是賠錢。
為了要解決這個問題,你需要做的是投資,而不單單只是存錢,指數化投資將會是首選。。
保險
台灣人很喜歡買保單,舉凡醫療險、投資型保單或是儲蓄險等,都是國人常買的險種。儘管我在著作<一年投資5分鐘>提到關於保險的購買原則,是讓它回歸保險的本質,但依然有不少投資朋友,將保險結合投資理財,讓原本不複雜的內容,變成複雜。
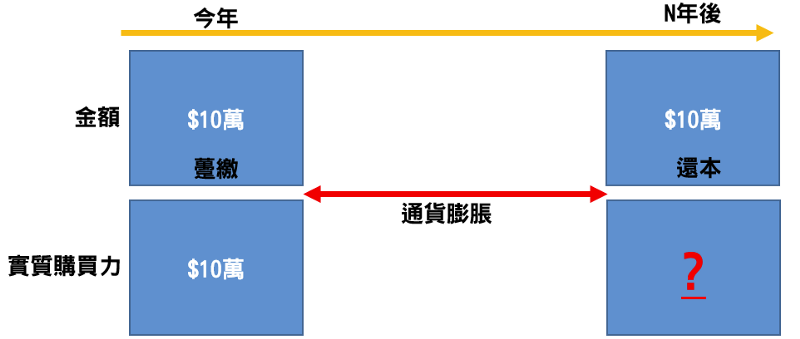
其中,有些保險類別又包含保本以及不保本,我所想強調的部分即是所謂保本的保單。
他的概念大概是這樣,如果你在保險期間沒有任何風險轉嫁,在保單結束或是生命終期之後,會歸還你所付出的保費,有的甚至還會高一些。
當我們乍聽之下,會覺得還本的保險還不錯,因為他們將錢還給了我們,還附帶中間的些許保障。
但是我必須要清楚地強調一點,還本保單的本,早已不是你的本了。
可是許多保險的朋友,沒有意識到這一點。他們認為能夠拿回原本付出的保費,就已經心滿意足。可是問題就在於,幾十年後再拿回來的金錢,早已不能與當年的價值相提並論。況且,當你以為你沒有付出任何保費就能獲得保險的內容,其實這之間經過折現率的價值,保險公司早就拿下了這無形的價值,對他們來說,純粹是用不同的收費方式,讓你付出無形的保費,而你有所不知。
因此,關於保險,我始終認為讓保險回歸人身保障的功能,而且千萬要記住,保險是要付出成本(金錢),如果你想要擁有足夠的保障,則採取定期險+投資理財的方式,加深未來自己的口袋,我相信會是更好的選擇。
財務規劃
在日常生活中,除了通貨膨脹以外,投資也離不開折現率的範疇。
從先前比較折現率高低的例子來說:
- 10%的折現率: 現在的100元會等於30年後的17449元
- 1%的折現率: 現在的100元會等於30年的1347元
我們可以說,當折現率越大,表示未來的貨幣價值將會越來越低,而從另一個角度來看,則是現在的貨幣非常值錢,這點更為重要。
尤其是針對債務。
就好比你今天跟銀行借了100元,銀行說30年後你必須償還17449元,你肯定會大罵,這根本是搶劫,但在銀行的眼裡,這筆當今的100元,可是擁有每年10%的機會成本,這也是銀行認為這筆資金的折現率。
然而,我們只要把握兩個原則,就有機會能減少我們的實質債務並且活用。
- 資金折現率 > 債務利率
- 越晚還越好
第一點,這邊的折現率可以當作是一個機會成本,一旦你能夠將債務的資金,轉化成折現率的成長結果,這筆債務其實會替你帶來正向的資金流,是會讓你賺錢的債務。
比如你借了1%利率的資金,但是如果在未來,你透過投資獲得2%的資金成長,這即是賺錢。
因此,當你對於這筆資金所實現的折現率(機會成本)高過債務利率,此債便是一個好債,將帶來正向的現金流。
第二點,債務還有另一項特點,就是還錢的時間點,當我們撇除利息這項因素,你應該明瞭,如果可以選擇償還債務的時間,越晚還對我們越有利。
為什麼呢? 我們可以想想看。
假如今天你跟銀行借了100元,銀行除了佛心不算利息之外,還讓你選擇還款的日期,你會選擇明天還是10年之後才還呢?
當我們選擇更遠的將來才償還,其背後的涵義,更是代表,我們將未來越沒有價值的錢,借到現在當作有價值的錢來使用。
就像之前所說的,30年的100萬能買下一棟房子,那時候的你,如果可以跟銀行借到30年後現在的100萬,也就是借100萬過了30年後才還,人生將會有非常不同的結果,對吧。
因此,關於財務規劃中的債務,也離不開折現率範疇,或者是說,對於擁有債務的人來說,折現率是一個非常重要的思考要點。
折現率 結論
折現率的觀念,經過這篇文章的說明,相信你一定理解,折現率其實與我們日常生活息息相關,尤其是在投資理財的相關領域,因為它可以化身為各種利率、也可以是個機會成本。
除非我們能讓時間停止,不然只要經過時間的變化,貨幣的價值就會有所差異,而折現率就是為此而生,讓我們可以擁有一個方法,評斷不同時空的貨幣價值,更是一座時間與價值的橋樑。
然而,要凸顯折現率應用最顯而易見的例子,莫過於通貨膨脹了。
當我們為了要維持相同的購買力,我們必須趕上通膨率,無論是增加人力資本或是透過指數化投資,不斷地增加資產,才能保持相同的生活水平。但從另一個角度來看,一旦你有能力將未來的錢拿來現在使用,那便是對貨幣使用了浴火重生之術,大幅提升它的內在價值了。
請記得,現在的貨幣將會比未來還值錢。
延伸閱讀:


2 則評論
YP大您好,”貼現率怎麼算?”這段最後的計算是不是多了一位數?
不好意思,請問您指的是哪個算式跟數字呢?