如果那一年我就知道..我就會選擇單筆投資而不是定期定額
投資要勇敢『 單筆投資 』還是『 定期定額 』?
2016年是我第一次接觸到投資理財的時間點,那時候我擁有一點小儲蓄,閱讀尋找許多關於投資方法的資料,最後下定決心採用長期投資指數化的方式,建構我的理財計畫。那時候的背景我記得很清楚,美股剛突破新高,而VTI的價位大概是110左右,歐洲市場跟新興市場則是距離高點下跌了不少,長期公債EDV則是來到新高140左右,那時候看著這些市場的狀況,我心中的想法是美股剛突破新高,年底又有總統大選,價位是不是太高啦,要不要等他跌下來再買一點;而面對歐洲跟新興市場又是覺得現在是下跌的趨勢耶,要不要等他止跌再買。基於以上的想法,我並沒有選擇單筆投入,因為我害怕,害怕買了就下跌,因此我規劃一年的時間將資金陸續投入到市場中。
現在回頭看起來,覺得很可惜。如果我早一點看到等等介紹的這篇文章,那我會毫不猶豫的單筆買進,但是這多少也是有點事後諸葛的心態,畢竟如果現在的市場狀況比當時還慘,我可能又會慶幸自己有留著資金做投資也說不定,因為你留著現金就是準備等它下跌再投入不是嗎?
然而,不管是你已經在投資或是打算投資的朋友,請花點時間好好閱讀這篇文章,理解文章所描述的內容,我相信絕對可以讓你理解為何單筆投入就過去的經驗會比分批投入還來的好。
上一篇我們從 Vanguard在2012的數據統計知道
- 單筆投入(Lump Sum)績效勝過分批投入(DCA)的時間高達66%
勇敢投入 vs 謹慎分批
而此篇為了可以更加說服你關於此論點,因此準備了許多數據跟圖表,你準備好接受洗禮了嗎?
如果還沒,請先深呼吸,好,來吧!
當我們要比較一次投入跟分批買進的勝負,其實我們要比的就是兩者在”分批投入的時間週期”中資產的成長,這個時間周期可能是一年、兩年,而我們要比的就是這個時間結尾的時候,兩者資產的高低。沒錯吧?因為一旦分批投入的時間周期結束,兩者其實會共同面臨市場的漲跌,也就無關勝負了。
因此,我們試著採用60/40(股票/債券)的資產組合,回測1960–2018區間,分批投入時間週期從2個月到60個月(五年)做為比較的變數。
下列的圖表中,每個點都表示DCA(分批投入)12個月對照單筆的績效比較表
- 0%以下的點表示分批投入輸給單筆買進
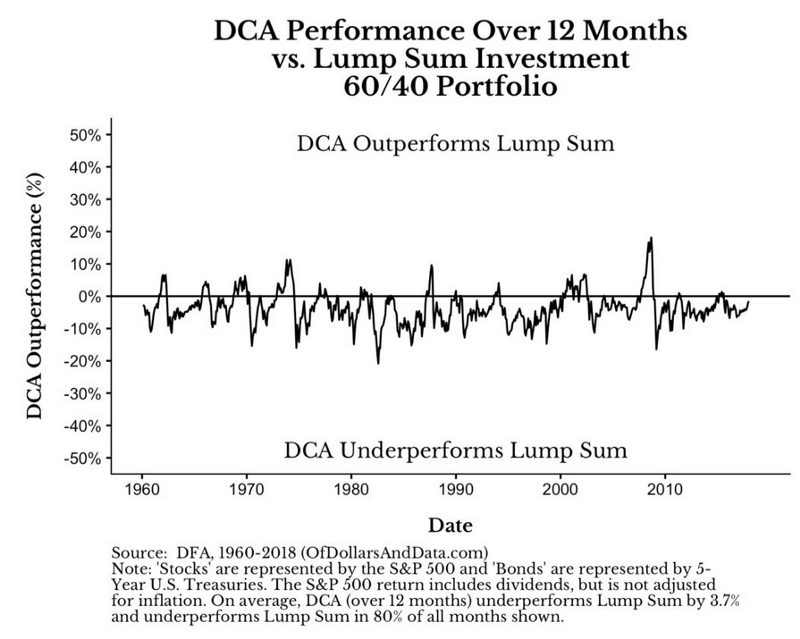
- 80%的時間,DCA輸給單筆投入
- DCA最突出的績效發生在2009年經濟危機落底前刻(市場下跌)
- 2009年落底之後,單筆投入立即就勝過DCA(市場上漲)
如果我們把DCA對比單筆投入的績效做個統計
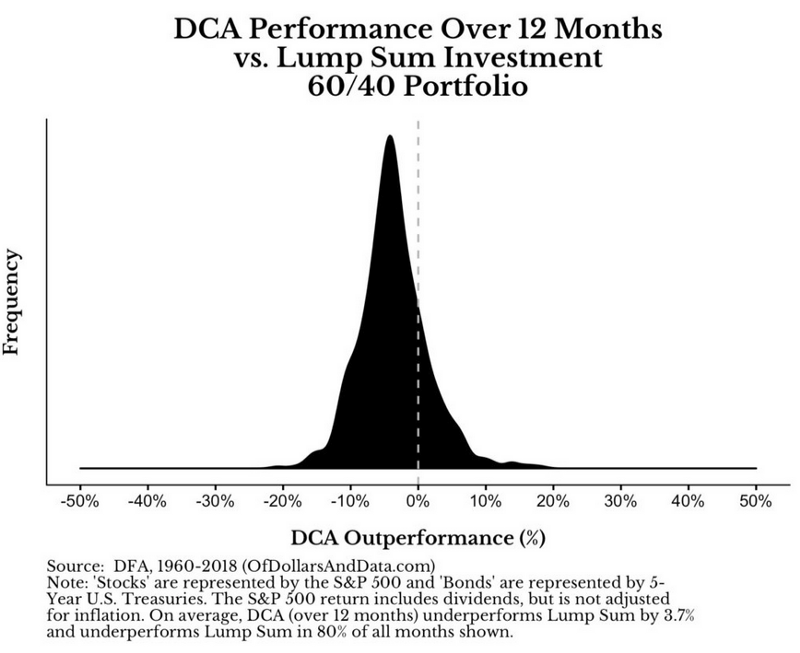
- 平均績效是 -3.7%,儘管績效大部分落在-5%~-10% -> 分批投入輸很多
- 這看起來似乎就是像常態分布
也就是說,你擔心市場下跌的狀況其實會被上漲的狀況抵銷,而且上漲的機率高很多,當你看到平均DCA的績效是負值,就能理解市場上漲的時間是比較多的。
如果覺得使用12個月的時間投入太過於短暫,想要更長的時間來驗證。沒問題,當你試著拉長時間週期,DCA的勝率沒什麼太大變化,但是敗率卻隨著時間拉長而快速上升。尤其是當超過24個月(或更長),相對的績效表現更是一蹋糊塗。
你可以從下方的動畫來檢視這樣的狀況(週期從2月-60月)
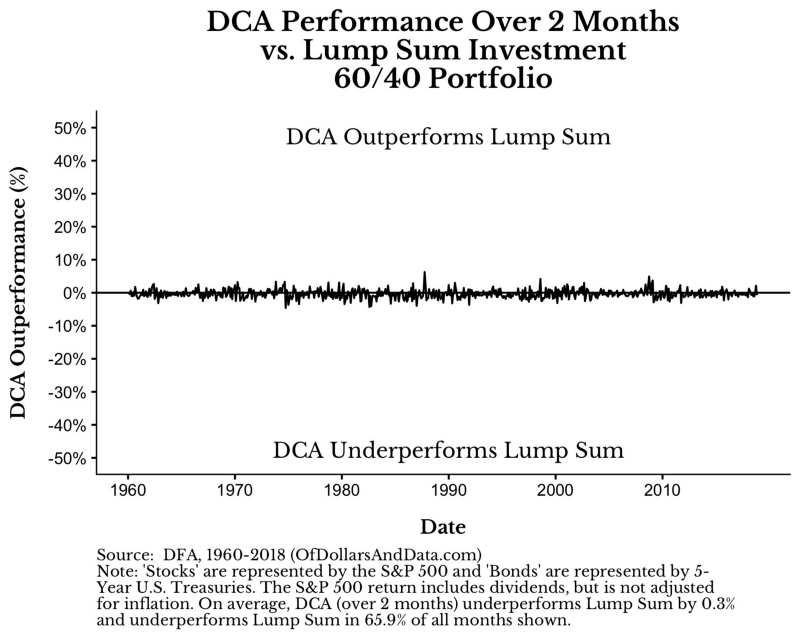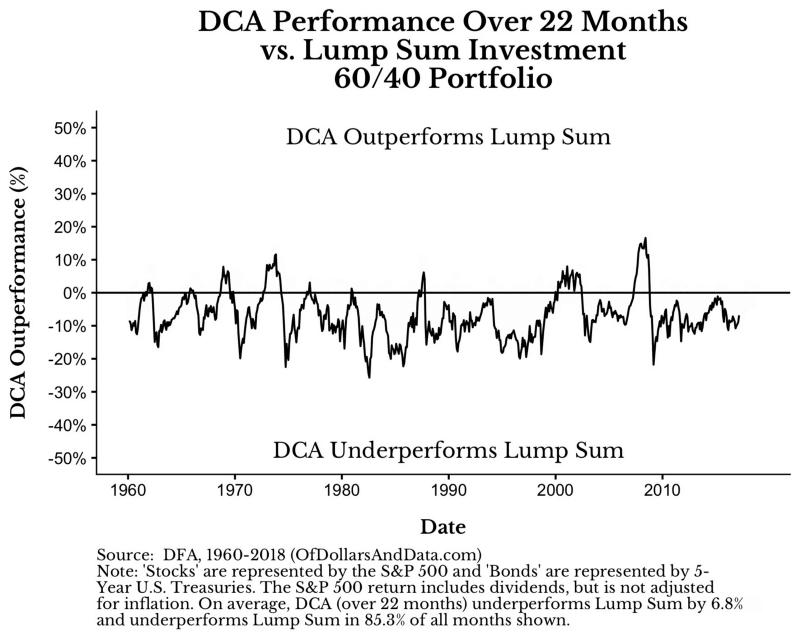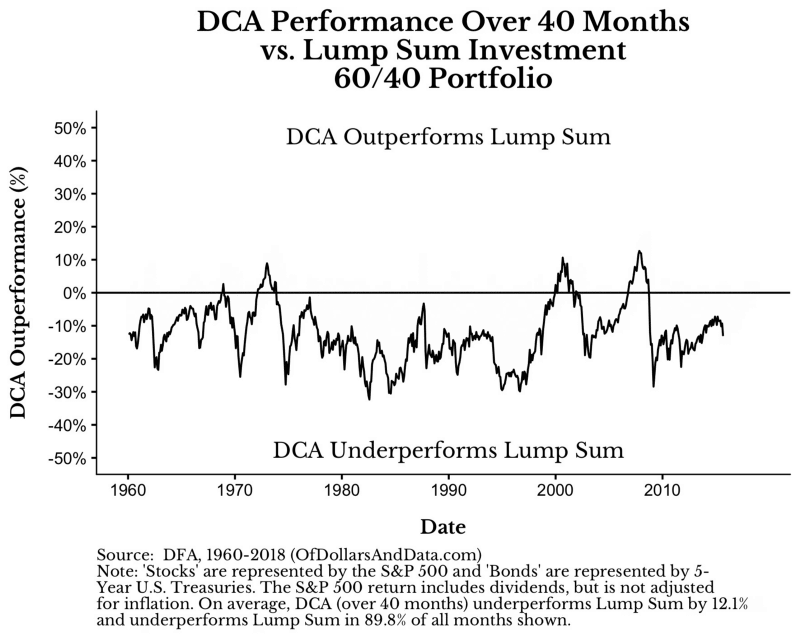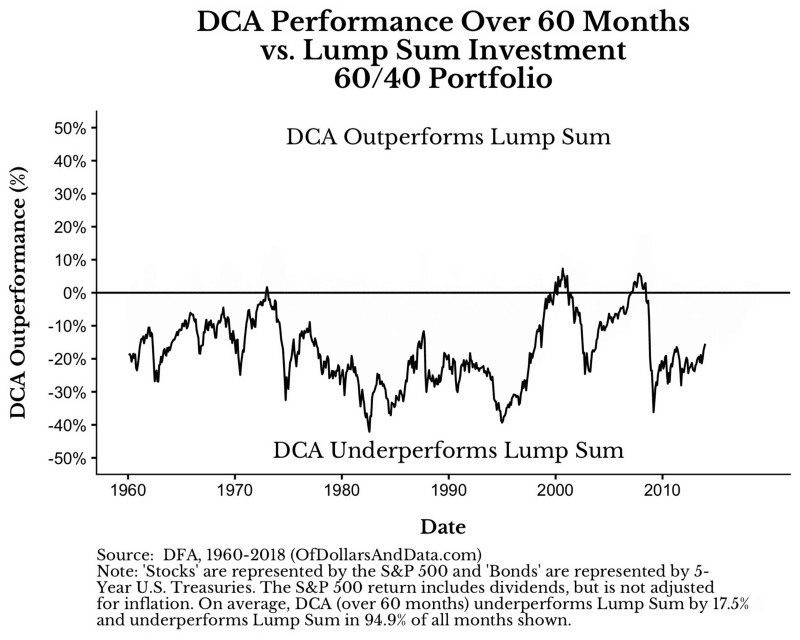
如同你所看到的線條動畫逐漸往下的現象,DCA的績效隨著分批投入時間增加而下滑。當你把時間拉長到分批投入五年之久,DCA敗給單筆投入的時間高達95%,而且平均輸17%績效。
你可以從下圖更直接觀察到分批投入績效分布狀況
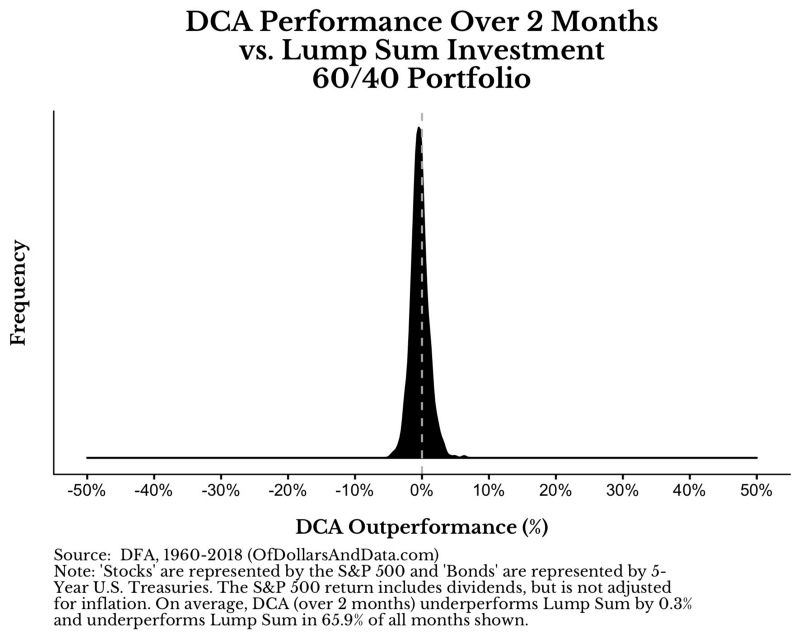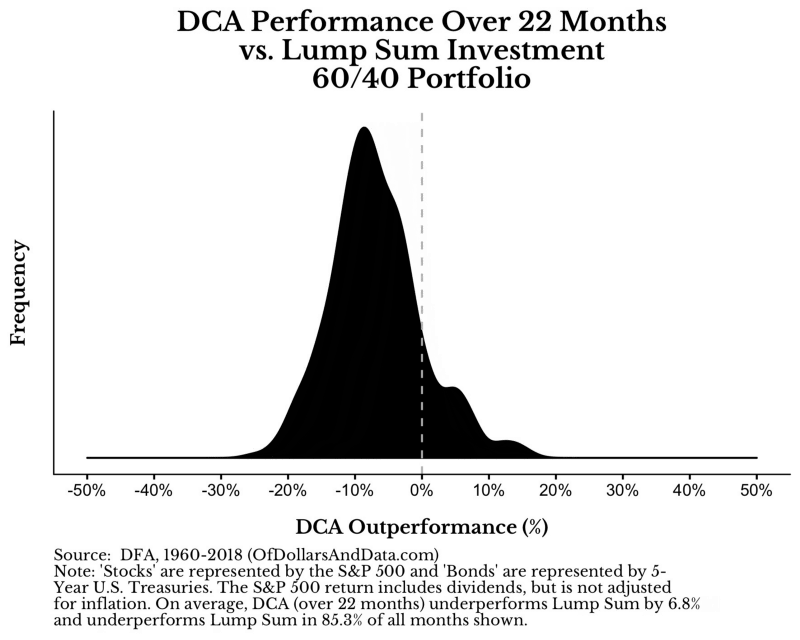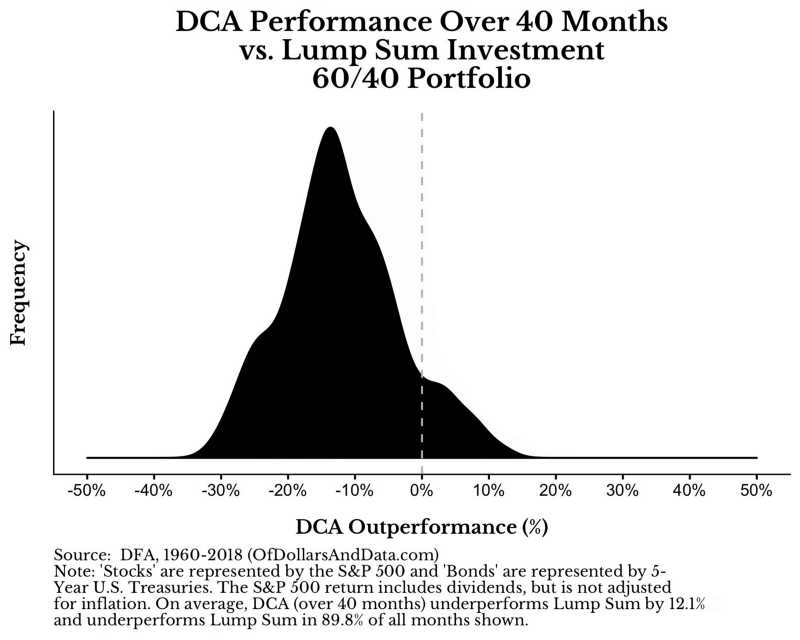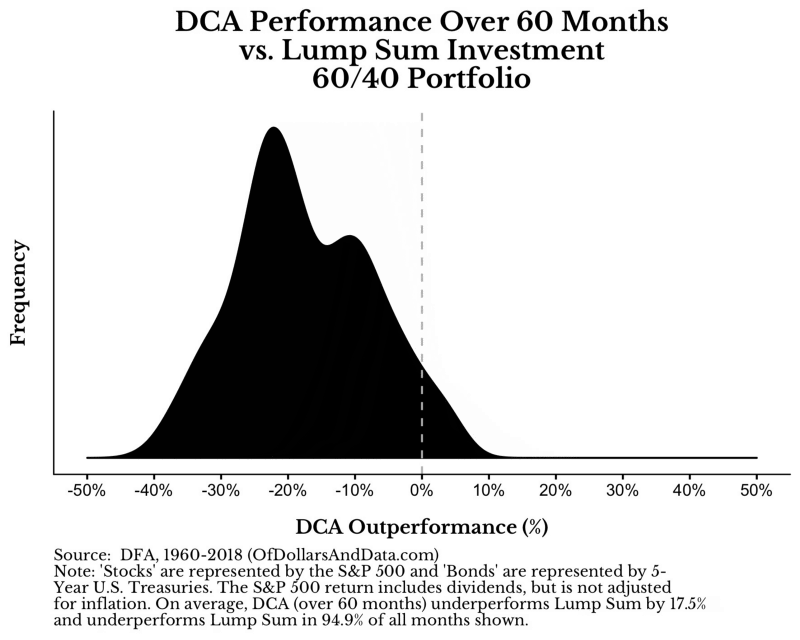
這就是你花時間分批投入所帶來的嚴重問題。
我們撇開過於長的時間週期,專注於兩年分批投入的狀況
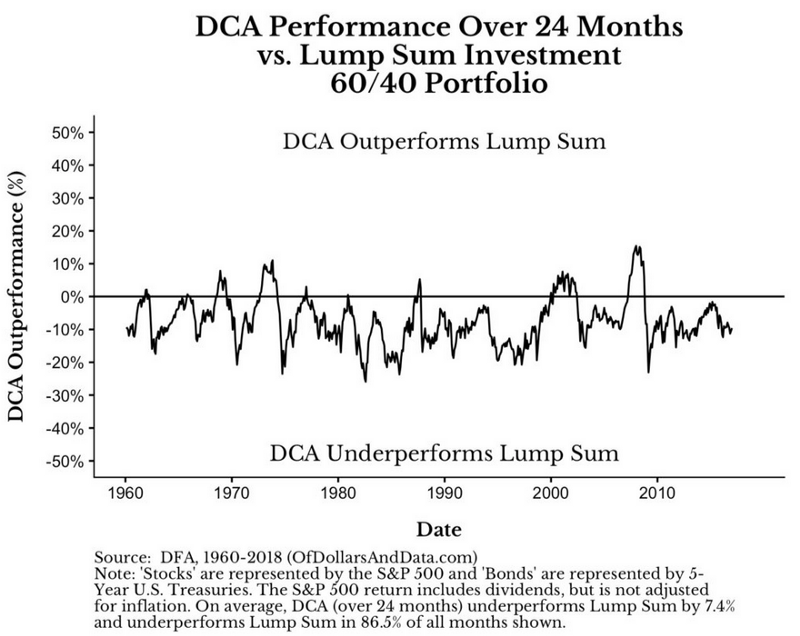
你可以看到在0%以上,也就是分批投入勝過單筆投入的次數,寥寥可數。你真的覺得你自己夠幸運可以在這些時間堅持做這些事情?你得知道,當DCA贏過單筆投入的時候其實就是市場下跌的狀況。
我們來看看這兩者的絕對報酬,藍色是單筆投入,黑色是DCA
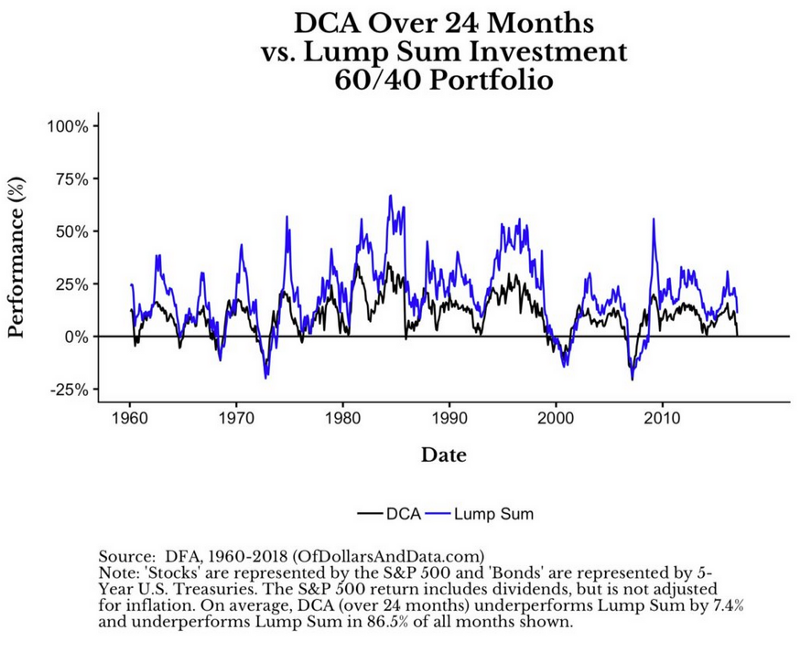
這樣夠清楚嗎?
如果有人試著用上圖介紹某兩種投資工具或是方法,請你做選擇,你會選擇黑色線條嗎? 肯定不會。
那你還會選擇分批投入這筆資金嗎?
因此,藉由這樣的說明,你應該就有想通該怎麼做了。
延伸閱讀: 持有現金等待低點入場
最後,你會面臨單筆投入恐懼的另一個原因是,你並不清楚你的風險承受度。所以你會害怕下跌的太多,然而,不知道你是否有注意到在本篇文章中所採用的組合是60/40股債平衡的配置,當然你可以試著轉換成符合你的風險承受度的組合。因此,你究竟能夠承受多少程度的下跌呢?我相信除了你自己以外沒有人更清楚了。
因此,一旦你確定了自己的風險承受度,就選擇適當的組合,單筆投入吧!
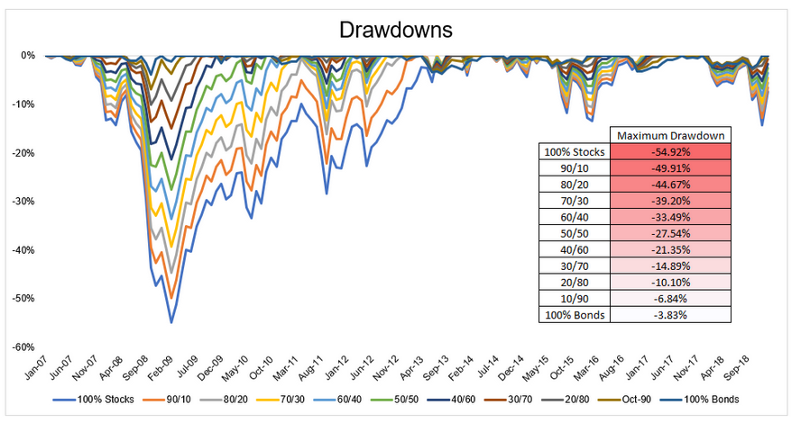
不同股債組合的歷史最大跌幅
人的一生就這麼一次,不管是身為一個人或是一個投資者,時間絕對是最重要的資產,千萬不要將時間白白浪費了。
主動生活,被動投資。
希望此篇文章可以解開你的疑惑,活出你的自我。
Reference: https://ofdollarsanddata.com/how-to-invest-a-lump-sum/
延伸閱讀:
